Pada posting sebelumnya sudah dibahas tentang menghitung kinerja algoritma klasifikasi dengan Confusion Matrix.
Tetapi confusion matrix hanya menyajikan informasi dalam bentuk angka. Untuk kasus klasifikasi 2 class (binary classification), jika ingin menampilkan informasi kinerja algoritma klasifikasi dalam bentuk grafik maka dapat digunakan Receiver Operating Characteristic (ROC) atau Precision-Recall Curve.
{Receiver Operating Characteristic / ROC}
Kurva ROC dibuat berdasarkan nilai telah didapatkan pada perhitungan dengan confusion matrix, yaitu antara False Positive Rate dengan True Positive Rate. Dimana:
- False Positive Rate (FPR) = False Positive / (False Positive + True Negative)
- True Positive Rate (TPR) = True Positive / (True Positive + False Negative)
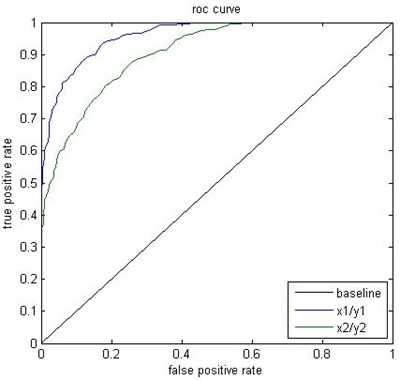
Dan berikut adalah contoh kurva ROC.
Untuk membaca kurva ini sangat mudah, kinerja algoritma klasifikasi adalah:
- JELEK, jika kurva yang dihasilkan mendekati garis baseline atau garis yang melintang dari titik 0,0.
- BAGUS, jika kurva mendekati titik 0,1.
Pada contoh di atas dapat dilihat 2 kurva, yaitu kurva dengan warna biru dan kurva dengan warna hijau. Berdasarkan cara membaca di atas, maka dapat disimpulkan kinerja kurva berwarna biru lebih bagus dibandingkan kinerja kurva berwarna hijau. Nah dengan cara seperti ini maka kita dengan mudah membandingkan bagus atau tidaknya teknik-teknik yang digunakan untuk menyelesaikan kasus klasifikasi pada suatu percobaan.
Selain itu jika ingin membandingkan nilai kinerja kurva biru dan kurva hijau dalam bentuk angka maka dapat dilakukan dengan membandingkan luas di bawah kurva atau Area Under Curve (AUC), dari gambar dapat dapat disimpulkan luas area kurva berwarna biru lebih besar dibanding luas area kurva berwar hijau.
Berikut ini adalah implementasi ROC dan AUC pada R. Package yang digunakan adalah ROCR. Untuk menginstall package ini digunakan perintah berikut ini.
1: install.packages("ROCR")
Pertama adalah menyiapkan data iris (yang memiliki 3 class) agar menjadi 2 class saja yaitu setosa dan virginica. Dan disiapkan juga data untuk training dan testing. Berikut adalah kode yang digunakan untuk keperluan tersebut.
1: data2class.train = rbind((iris[which(iris$Species == "setosa"),])[1:45,], (iris[which(iris$Species == "virginica"),])[1:45,])
2: data2class.test = rbind((iris[which(iris$Species == "setosa"),])[46:50,], (iris[which(iris$Species == "virginica"),])[46:50,])
3:
4: data2class.train = droplevels(data2class.train)
5: data2class.test = droplevels(data2class.test)
Selanjutnya adalah melakukan klasifikasi, pada contoh ini digunakan algoritma SVM dengan menggunakan fungsi ksvm() dari package kernlab.
1: library(kernlab)
2:
3: model = ksvm(Species~., data2class.train)
4: predict_result = predict(model, data2class.test[,-5])
Kemudian untuk menghitung kinerja digunakan fungsi-fungsi dari package ROC berikut ini.
1: library(ROCR)
2:
3: roc.prediction = prediction(as.numeric(as.factor(predict_result)), as.numeric(as.factor(data2class.test[,5])))
4: roc.tpr.fpr = performance(roc.prediction,"tpr","fpr")
5: roc.auc = performance(roc.prediction,"auc")
Untuk menggambar kurva ROC berdasarkan hasil perhitungan di atas digunakan kode dibawah ini.
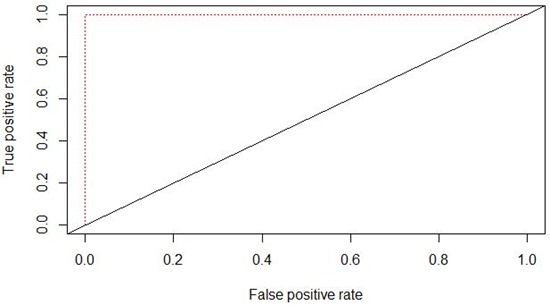
1: plot(roc.tpr.fpr, col="red",lty=3)
2: abline(a=0, b= 1)
Berikut adalah kurva ROC yang dihasilkan.
Dan untuk menampilkan hasil perhitungan AUC digunakan kode berikut ini.
1: print(paste("Luas AUC:", roc.auc@y.values))
Dan nilai yang didapatkan adalah:
1: "Luas AUC: 1"
Dari kurva ROC dan nilai AUC di atas dapat disimpulan bahwa kinerja algoritma SVM untuk kasus dataset Iris dapat memprediksi seluruh data test dengan sempurna.
{Precision-Recall Curve}
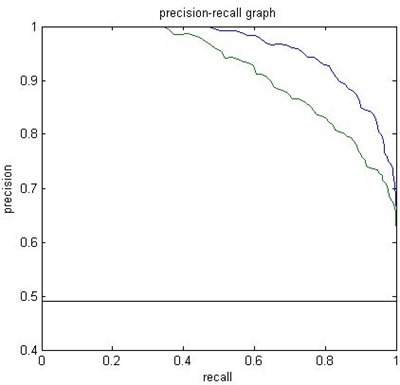
Menurut beberapa literatur, jika kita menemui kasus dimana class positive (yang biasanya berjumlah sedikit, atau minority class) maka yang cocok digunakan sebagai teknik untuk menggambar kurva kinerja adalah Precision-Recall Curve. Kurva ini dibuat berdasarkan nilai telah didapatkan pada perhitungan dengan confusion matrix, yaitu antara Precision dan Recall, dimana:
- precision = True Positive / (True Positive + False Positive)
- recall = True Positive / (True Positive + False Negative)
Dan berikut adalah contoh kurva Precision-Recall.
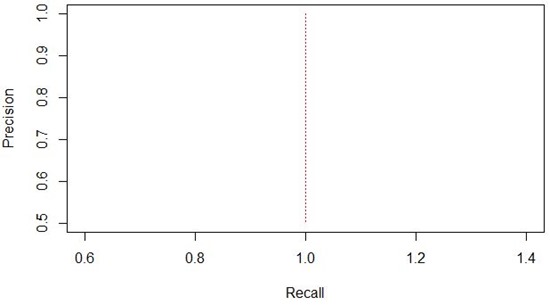
Kode R yang digunakan untuk menghitung precision dan recall kemudian menggambarkannya dalam kurva adalah sebagai berikut.
1: library(ROCR)
2: roc.prediction = prediction(as.numeric(as.factor(predict_result)), as.numeric(as.factor(data2class.test[,5])))
3: roc.prec.rec = performance(roc.prediction,"prec","rec")
4:
5: plot(roc.prec.rec, col="red",lty=3)
Dan hasilnya adalah sebagai berikut.
Nah gampang kan. Selamat mencoba ![]()